Сумма градусов треугольника - это фундаментальное понятие в геометрии, которое устанавливает взаимосвязь между углами любой треугольной фигуры. Данное свойство является постоянным для всех типов треугольников в евклидовой геометрии.
Содержание
Основная теорема о сумме углов треугольника
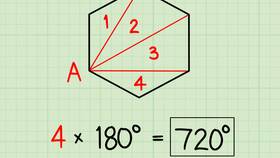
В евклидовой геометрии сумма внутренних углов любого треугольника всегда равна 180 градусам. Это утверждение известно как теорема о сумме углов треугольника и является одной из базовых теорем планиметрии.
| Тип треугольника | Сумма внутренних углов |
| Остроугольный | 180° |
| Прямоугольный | 180° |
| Тупоугольный | 180° |
| Равносторонний | 180° |
| Равнобедренный | 180° |
Доказательство теоремы
Рассмотрим простое доказательство этой теоремы:
- Нарисуем произвольный треугольник ABC
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при вершине B составят развернутый угол (180°)
- Эти углы равны соответствующим углам треугольника (как накрест лежащие)
- Следовательно, сумма углов A, B и C равна 180°
Следствия из теоремы
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
- В прямоугольном треугольнике два острых угла в сумме дают 90°
- В равностороннем треугольнике все углы равны 60°
- Максимальный угол в треугольнике не может быть меньше 60° (в невырожденном случае)
Особые случаи
| Сферический треугольник | Сумма углов превышает 180° |
| Гиперболический треугольник | Сумма углов меньше 180° |
| Вырожденный треугольник | Сумма углов равна 180° (но все точки лежат на одной прямой) |
Практическое применение
Знание суммы углов треугольника широко используется в геодезии, архитектуре, строительстве, навигации и компьютерной графике. Оно позволяет вычислять неизвестные углы, проектировать конструкции и решать различные прикладные задачи.